yuca
Life in Lenia
Cellular Automata (CA)
In general CA are dynamic systems that change due to rules applied in a local context.
i.e. compute neighborhood > compute update
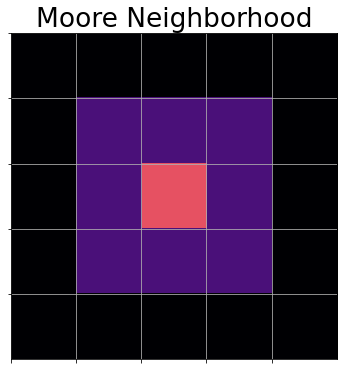
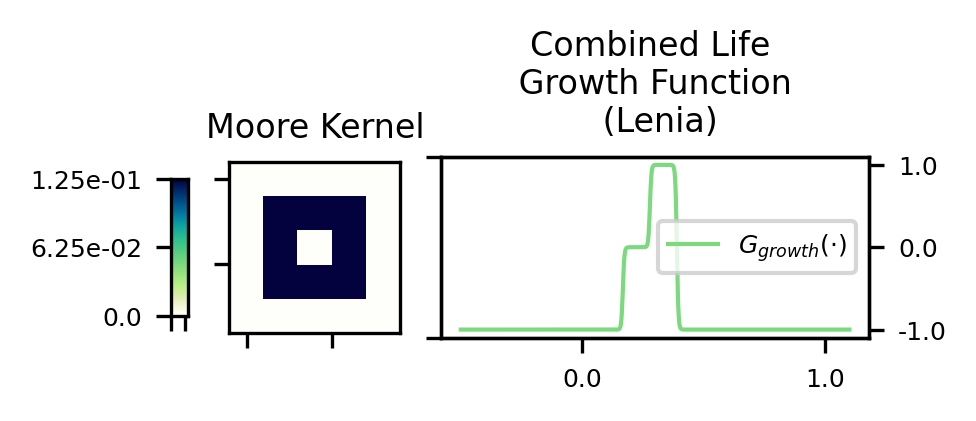
Lenia
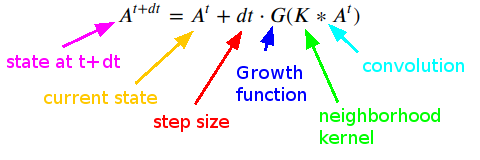
In Lenia, the neighborhood is defined by a smooth, continuously valued convolution kernel with a transition update defined by a smooth function called a Growth function (usually a Gaussian)
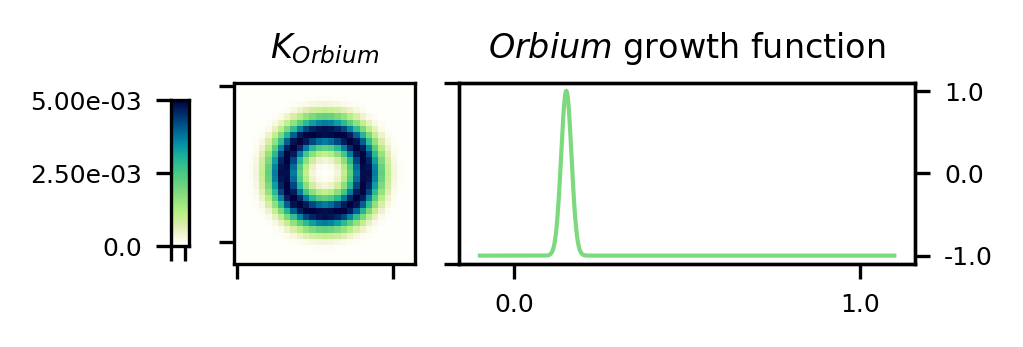
The update takes the essential form of Euler’s numerical method for differential equations.
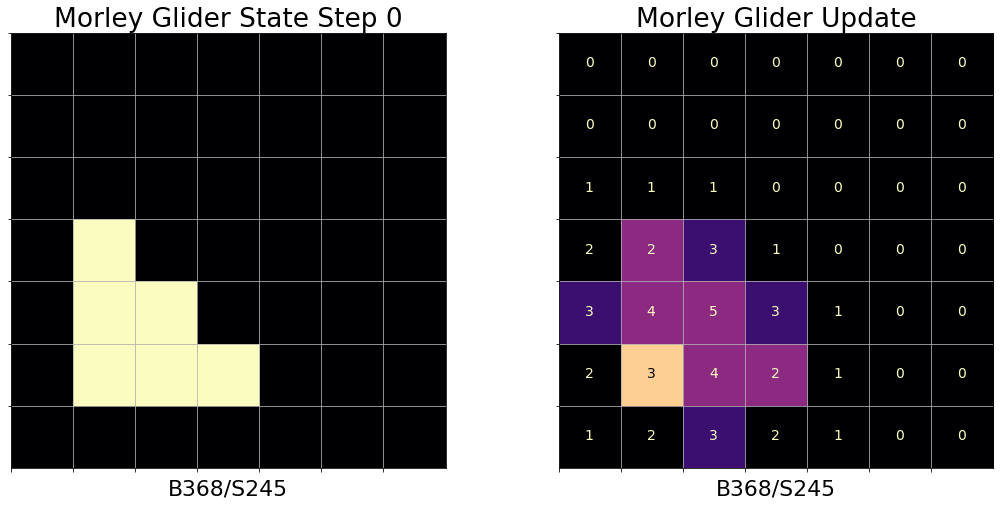
Life in Lenia
In words, the B3/S23 Life rule: if a cell has exactly 3 neighbors it becomes a 1, if it has 2 or 3 neighbors it keeps its current value, and if it has any other number of neighbors it becomes 0.
The Lenia framework can easily represent Conway’s Game of Life with a Moore neighborhood convoluton kernel and smooth step functions corresponding to B3/S23.