Hi

A few days ago I described a project comparing simulating Life-like cellular automata in the Julia programming language to simulation in Python using PyTorch. The initial impression was not particularly favorable to Julia, but the comparison wasn’t based on equivalent implementations and both methods had some easy speed improvements left on the table. Cleaning up the Julia implementation, particularly removing a line that performed an extra Fourier transform convolution where only 1 was intended, led to execution speeds more than 100% faster. I also wrote a new implementation in NumPy that is much closer to the Julia implementation, using numpy.fft methods to perform convolutions.


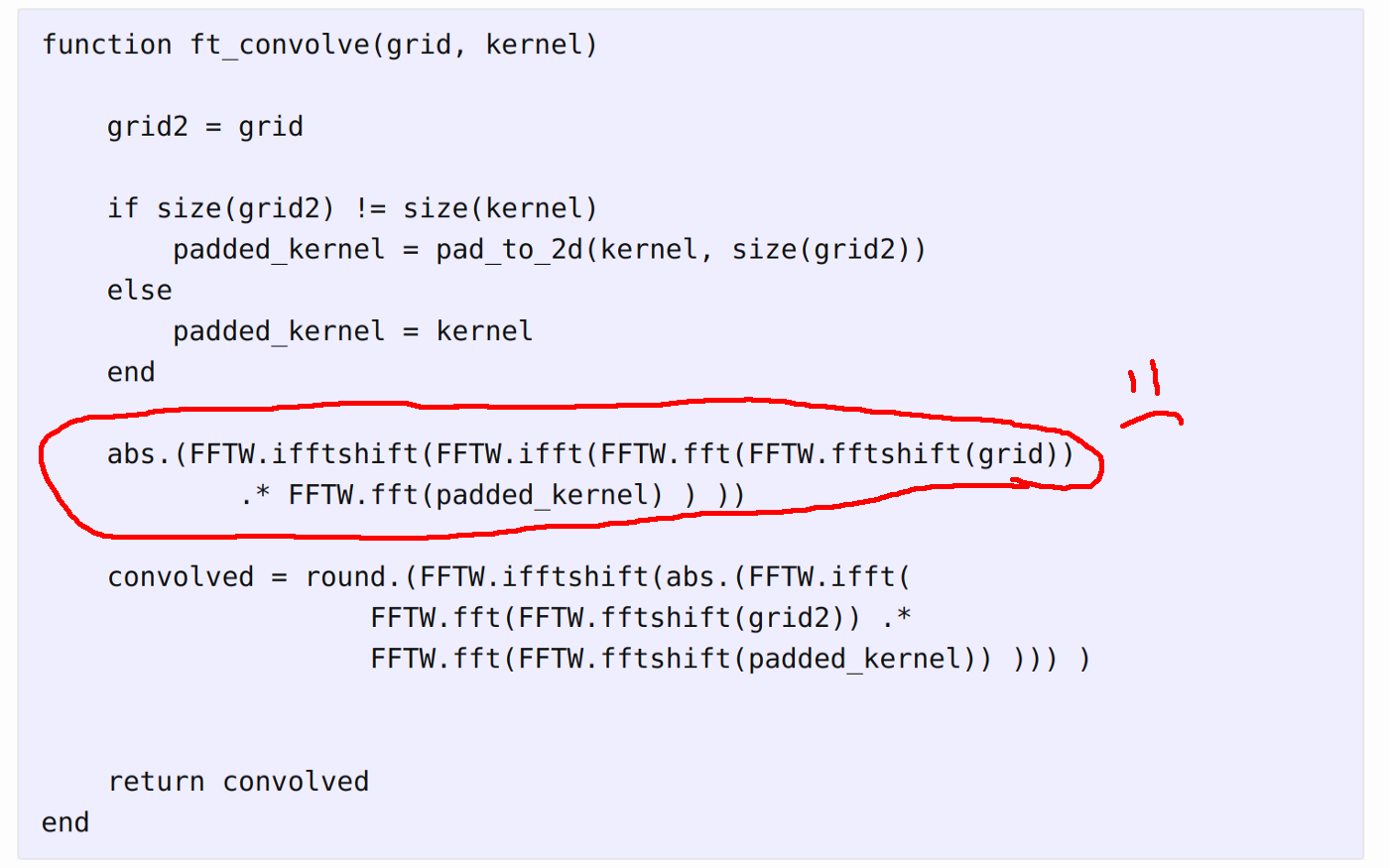
A mistake in the Julia CA simulator


I also updated my PyTorch version from 1.5.1 to 1.9.0 for a significant speed up in CA simulations with CARLE, and I moved the benchmark code into stand-alone scripts because running the same code in Jupyter notebooks was giving me inconsistent timing results. With these changes my Life simulator in Julia is now the fastest of the 3 implementations for a grid size of 64 by 64, while CARLE is faster for grid dimensions of 128 to 1024 cells and NumPy is consistently the slowest.

An interesting pattern emerges when comparing the scaling characteristics of the PyTorch CA simulator CARLE, to scaling seen in both the NumPy and the Julia implementations. Using PyTorch and the Conv2D functionality in torch.nn, execution speeds scale at a roughly linear rate. In NumPy and Julia where I used Fourier transforms to perform convolutions, on the other hand, the scaling looks exponential.


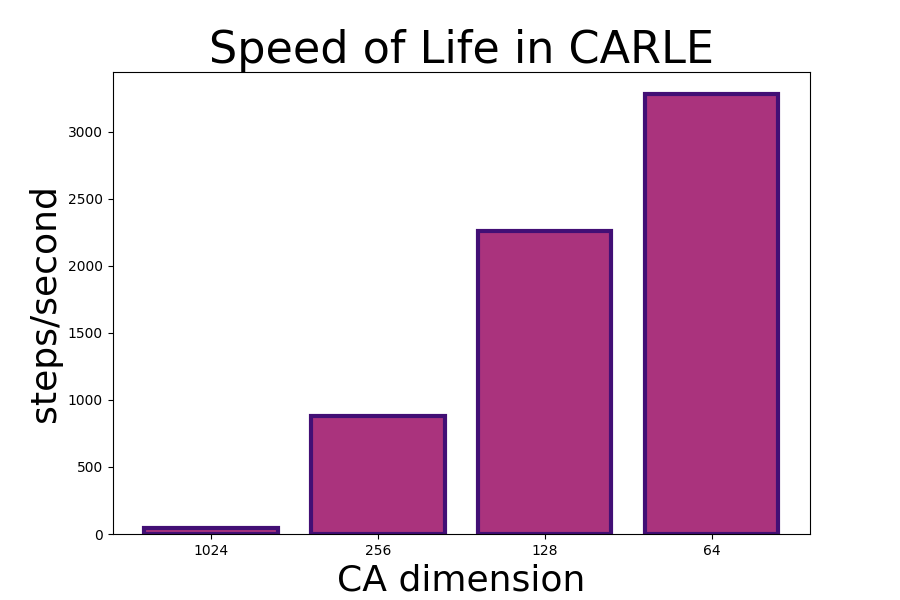
CA steps per second for grid side-lengths of 1024, 256, 128, and 64 using a PyTorch implementation, CARLE. Note the approximately linear scaling. This figure shows execution speeds on a 4-core laptop CPU.

CA steps per second for grid side-lengths of 1024, 256, 128, and 64 using a NumPy implementation. This figure shows execution speeds on a 4-core laptop CPU.

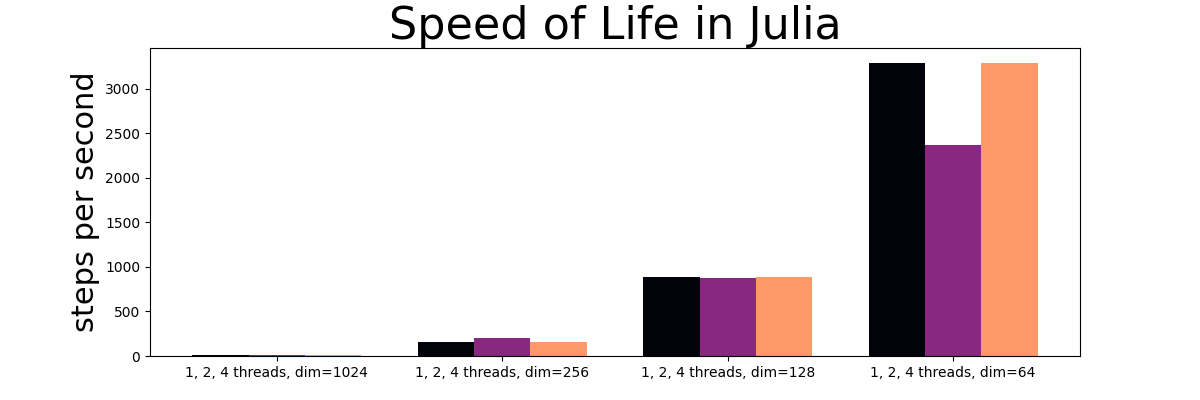
CA steps per second for grid side-lengths of 1024, 256, 128, and 64 using an implementation in Julia. This figure shows execution speeds on a 4-core laptop CPU.


The different scaling characteristics reflect the differences in how convolutions are performed internally in PyTorch and in my FFT-based code. This suggests that there should be a significant speed advantage and more favorable scaling behavior to be had by using a more comparable Julia machine learning library like NNLib (as pointed out in this comment on GitHub). It’s something I’ll be looking into more closely in the future.

Results

Upgrading from PyTorch 1.5.1 to 1.9.0 increased the execution speed in CARLE from 2087, 1216, and 519 steps per second in grids with side-lengths of 64, 128, and 256 cells to 3280, 2259, and 877 steps per second. That equates to a range of about 57% to 85% speedup. In Julia, removing the line containing an extra FFT-based convolution led to speedups for the same grid sizes from 82 to 210, 425 to 882, and 1462 to 3292 steps per second, or about 107% to 256% speeds more than 100%. Some of the improvement may have also been the result of moving the benchmark code to stand-alone scripts, as running the same code in Jupyter notebooks has some additional overhead and was yielding inconsistent run-times.

Laptop CPU

grid dimensions Julia (1 thread) Julia (2 threads) Julia (4 threads) NumPy CARLE units
1024 by 1024 5.65 7.61 7.37 5.56 46.48 steps/second
256 by 256 162.33 197.34 201.67 157.21 877.69 steps/second
128 by 128 882.73 873.14 854.00 641.38 2259.33 steps/second
64 by 64 3292.31 2372.21 1966.58 1831.78 3280.93 steps/second
Table of execution speeds on a 4-core Intel i5-6300U laptop CPU

Desktop CPU

grid dimensions Julia (1 thread) Julia (2 threads) Julia (4 threads) NumPy CARLE units
1024 by 1024 6.51 12.08 16.22 8.98 221.64 steps/second
256 by 256 159.15 172.85 210.43 229.16 1735.07 steps/second
128 by 128 1037.14 898.17 918.44 999.98 2722.23 steps/second
64 by 64 4839.79 2722.67 2301.78 3050.90 4437.3 steps/second
Table of execution speeds on a 24-core AMD Threadripper 3960x desktop CPU