yuca

Selecting Continuous Life-Like Cellular Automata for Halting Unpredictability: Evolving for Abiogenesis

Q. Tyrell Davis and Josh Bongard

• Blog post (you are here)
• ArXiv -> https://arxiv.org/abs/2204.07541
• Summary poster
• Bokeh app glider demo – watch evolved gliders Note that this runs on mybinder.org, a great free cloud notebook service that can be a little slow. ArXiv -> https://arxiv.org/abs/2204.07541

Summary

If you wish to make an apple pie from scratch, you must first invent the universe. ---Carl Sagan _Cosmos_ 1980

¹

Lucky for pie-lovers everywhere, we already have a universe with all the physical laws and pre-requisites for the existence of a wide range of baked goods and bakers to make them. That’s convenient, because universe creation is not in our experimental repertoire, at least for the type of universe we reside in. We can, however, reason about and experiment with general principles for the emergence of life-like or bioreminiscent characteristics in simplified, artificial worlds, and in this work we focus on continuously-valued cellular automata (CA) as our substrate.

Recent work in continuous CA, in particular in the Lenia framework ², has generated a vast taxonomy of bioreminiscent patterns. To date this has mostly been the product of manual exploration and human-directed interactive evolution [^Ch2018]³, resulting in 100s of life-like patterns (or “pseudorganisms”) that move, interact, and maintain self-integrity to some degree. Limiting exploration of continuous CA to manual or semi-automated methods may limit the diversity of results ⁴, which may in turn limit the ideas considered as falsifiable hypotheses as the study of ALife in continuous CA matures.

Complicated and carefully engineered CA systems in the tradition of John Von Neumann’s universal constructor CA ⁵ can display life-like characteristics such as self-replication, movement, and growth. On the other hand Conway’s Game of Life [^Be2004] and successors showed that very simple CA rules can give rise to complex systems with similar capabilities, and it seems that only minimal criteria need to be met in a simple complex system to achieve life-like traits and computational capability.

Unlike Von Neumann’s 29-state CA, we can describe the development of Conway’s Life as evolution via selection for human preferences. One of the selection criteria that emerged under and encompassing search for something interesting was the simultaneous support for opposing capabilities to grow without bound or to vanish completely. In fact the inability to predict whether a given pattern under a given set of CA rules will persist or vanish is in fact a version of the halting Entscheidungensproblem (decision problem).

In the article introducing the public to Conway’s Game of Life (In Martin Gardner’s ‘Mathematical Games’ column of Scientific American ⁶), a prize was offered for the first proof of a pattern in Life that exhibits indefinite growth. Quote is from a 2011 interview with John Conway by Dierk Schleicher ⁷. Image is adapted from photograph CC BY Thane Plambeck

The casual heuristic of persistent and vanishing patterns that Conway and colleagues employed become the basis for Eppstein’s fertility and mortality metrics. Eppstein’s treatment was even more lenient in that it suggests that any Life-like CA that has one or more patterns that grow outside initial bound (fertility) and one or more patterns that disappear (mortality) is likely complex enough to support universal computation ⁸⁹.

Working in the substrate of continuous CA (Lenia and a variant called Glaberish), in this work we automatically evolved CA rules, followed by a second stage of evolution to evolve patterns within the new rule sets. We applied selection via halting unpredictability (using a new ensemble of 3 conv-nets to try to learn halting prediction for each CA rule candidate. We also used a simpler selection criteria based on an even proportion of persistent and quiescent grids after a specified number of update steps, starting from a grid of random uniform cell states. Compared to random samples from the starting distributions of these CA rule sets (starting with values near those of the Hydrogeminium natans and Orbium Lenia rules), both halting unpredictability and halting proportion evolution yields more rule sets that support persistent gliders in a subsequent pattern evolution step. Given the additional computational resources of training an ensemble of neural networks for halting prediction vs simply counting the number of grids with and without live cells at the end, it seems that selecting for the simple existence of halting and growth patterns under typical circumstances is preferable to evolving halting unpredictability.

This blog post is a description of work presented as a poster and more thoroughly as an accompanying short paper at GECCO 2022. A library called Your Universal Cellular Automata (yuca) was developed for and used to run experiments, and you can evolve your own CA rules and patterns using the open sourced MIT-licensed code.

The work received funding from the National Science Foundation under the Emerging Frontiers in Research and Innovation (EFRI) program (EFMA-1830870)

Visual methods summary

Phase one: evolving CA rules

In this first phase, CA rules were evolved according to selection for halting unpredictability or roughly equal halting/persistence proportions in a batch of grids initialized from a random uniform distribution. We’ll refer to the first case as halting unpredictability evolution and the second a simple halting evolution.

‘Halting unpredictability’ was based on the (negative) average accuracy of an ensemble of convolutional neural networks trained to predict whether a CA pattern would persist or vanish (all cells go to zero) after a given number of CA steps. Simple halting was instead based on the total proportion of persistent versus vanished grids after a given number of time steps, specifically the difference between the proportion of persistent/vanished grids and an even 0.5/0.5 split.

An example command to run evolution with fitness based on halting unpredictability is

python -m yuca.evolve -b 64 -c 512 -d cuda -f HaltingWrapper -g 32 -p 64 -k 31 -l 3 -m 128 -s 42

The command above specifies (in order of flags) a batch size of 64, 512 CA steps, to run on GPU, halting unpredictability-based fitness, 32 generations, a population size of 64, 3 replicates (i.e. train 3 separate conv-nets per each episode), a grid dimension of 128 by 128, and a random seed of 42.

Using simple halting fitness is more economical in terms of computational resources, and seems to generate just as many glider-supporting CA as the more convoluted halting unpredictability fitness. The command is nearly the same:

python -m yuca.evolve -b 64 -c 512 -d cuda -f SimpleHaltingWrapper -g 32 -p 64 -k 31 -l 3 -m 128 -s 42

Phase two: evolving gliders

Gliders (here referring to mobile CA patterns in general) act as information carriers and can carry out computations in their collisions, and can be quite charismatic and/or aesthetically pleasing in their activity. A recent project described the nascent training of agency in Lenia-based gliders, which may provide the substrate for studying agency and learning under consistent physics (i.e. a glider operates under the same rules as its environment.

The glider evolution step in this project uses the same covariance matrix adaptation evolution strategy ¹⁰ as for evolving CAs, coupled with a fitness metric comprised of motility and homeostasis components and compositional pattern-producing networks for encoding starting synthesis patterns ¹¹. The motility component is calculated by finding the “center-of-mass” of active cells in the pattern, producing a positive reward when its position changes. A homeostasis component is a negative reward based on changes in the average cell value of all cells in the grid. Combined these metrics provide increased reward for patterns that move across the grid without growing too much or disappearing. There is also a large negative penalty for patterns that disappear before the simulation completes its run.

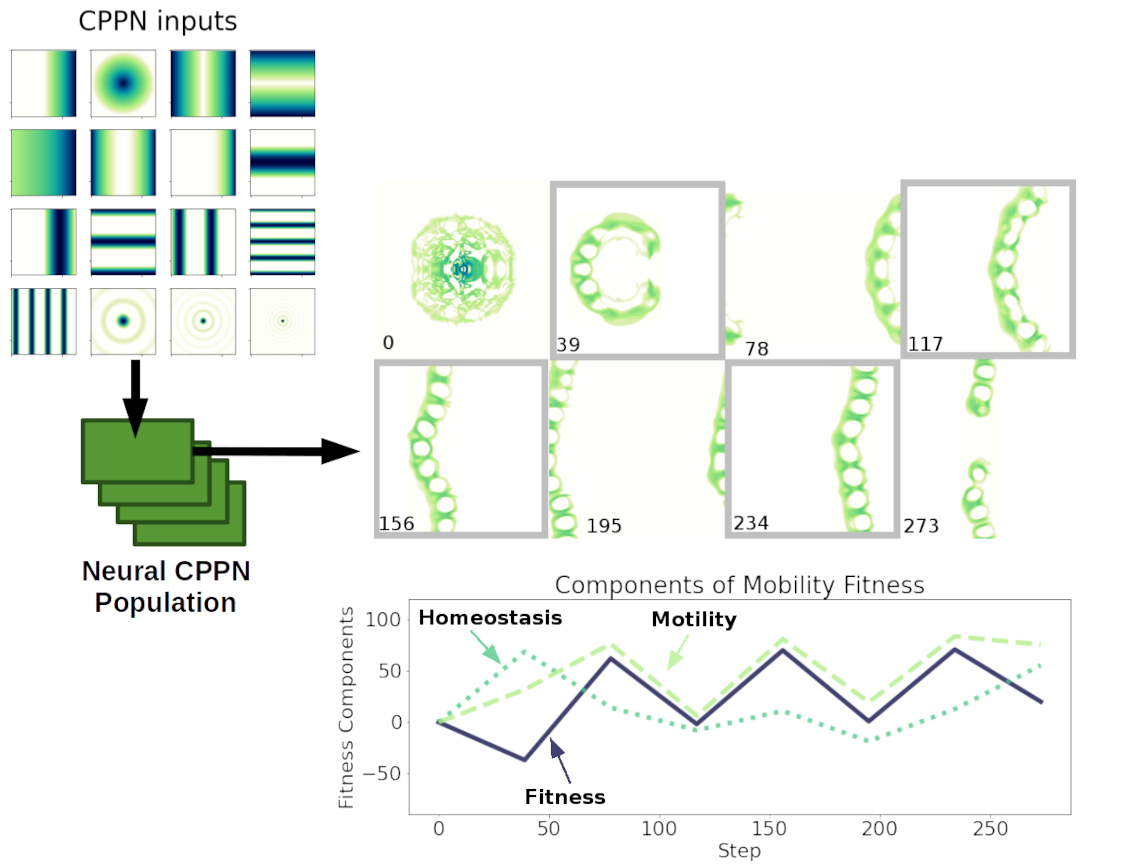
Glider evolution has the same entry point but uses a different reward wrapper. There’s no point in setting the replicates flag -l to a value other than 1, because each CPPN individual produces a static starting synthesis pattern.

python -m yuca.evolve -b 64 -c 512 -d cuda -f GliderWrapper -g 32 -p 64 -k 31 -l 1 -m 128 -s 42

Appendix 1: Re-discovered pattern zoo (Lenia patterns)

Most of the glider patterns evolved in Lenia CA were previously documented in ², ³, and in an online interactive demo: chakazul.github.io/Lenia/JavaScript/Lenia.html.

Hydrogeminium natans

Discutium solidus

Discutium valvatus

Scutium gravidus

Scutium solidus

Scutium valvatus

Paraptera sinus labens

Paraptera arcus labens

Orbium

Orbium unicaudatus ignis

Synorbium

Appendix 2: New patterns evolved in evolved CA

This section includes a selection of glider patterns that don’t resemble Lenia patterns, evolved under CA rules that were in turn evolved for halting/persistence or halting unpredictability. Other evolved rules yielded gliders as well, but with patterns that generally resembled previously described Lenia patterns (espeically Orbia)

Evolved CA s613 (halting unpredictability selection)

Evolved CA s643 (Simple halting/persistence selection)

Evolved CA s11 (Simple halting/persistence selection)

Unevolved CA (random selection)

This CA rule set was “unevolved” i.e. instead of selection for halting/persistence or halting unpredictability, fitness was assigned at random. Nonetheless the rule set was able to support the pseudo-glider pattern shown above, evolved with the same center-of-mass and homeostasis selection mechanisms as the gliders found in evolved CA rule sets. The pattern is only pseudo-stable, however, and undergoes several shape changes before breaking down.

1. Carl Sagan. Cosmos. Random House, New York. 1980. ISBN: 0-394-50294-9 p. 218 ↩

2. B. W.-C. Chan, “Lenia: Biology of Artificial Life,” Complex Systems, 28(3), 2019 pp. 251–286. https://doi.org/10.25088/ComplexSystems.28.3.251 ↩ ↩²

3. Chan, Bert Wang-Chak. “Lenia and Expanded Universe.” ALIFE 2020: The 2020 Conference on Artificial Life. MIT Press, 2020. https://arxiv.org/abs/2005.03742 ↩ ↩²

4. Consider the gap in diversity of domestic versus wild life. ↩

5. Neumann, John von and Arthur W. Burks. “Theory Of Self Reproducing Automata.” University of Illinois Press, Urbana and London. (1966). ↩

6. Gardner, Martin. “The Fantastic Combinations of John Conway’s New Solitaire Game’Life.” Sc. Am. 223 (1970): 20-123. ↩

7. Dierk Schleicher. Interview with John Horton Conway. 2011 https://www.ams.org/notices/201305/rnoti-p567.pdf ↩

8. Eppstein, David. “Growth and decay in life-like cellular automata.” Game of Life cellular automata. Springer, London, 2010. 71-97. https://arxiv.org/abs/0911.2890 ↩

9. There are exceptions that do not meet both criteria and yet are still capable of universal computation and interesting activity, many of which are mentioned in Eppstein’s paper. One example, Life without Death (B3/S012345678), is the antithesis of a mortal CA but does support computationally complete structures uses a kind of rod logic (e.g. https://conwaylife.com/forums/viewtopic.php?t=&p=106546#p106546 ) ↩

10. Auger, Anne, and Nikolaus Hansen. “Tutorial CMA-ES: evolution strategies and covariance matrix adaptation.” Proceedings of the 14th annual conference companion on Genetic and evolutionary computation. 2012. ↩

11. Stanley, Kenneth O. “Compositional pattern producing networks: A novel abstraction of development.” Genetic programming and evolvable machines 8.2 (2007): 131-162. ↩

This site is open source. Improve this page.