Faster Convolutions and Cellular Automata in Julia with NNlib: 2.7X Faster than PyTorch

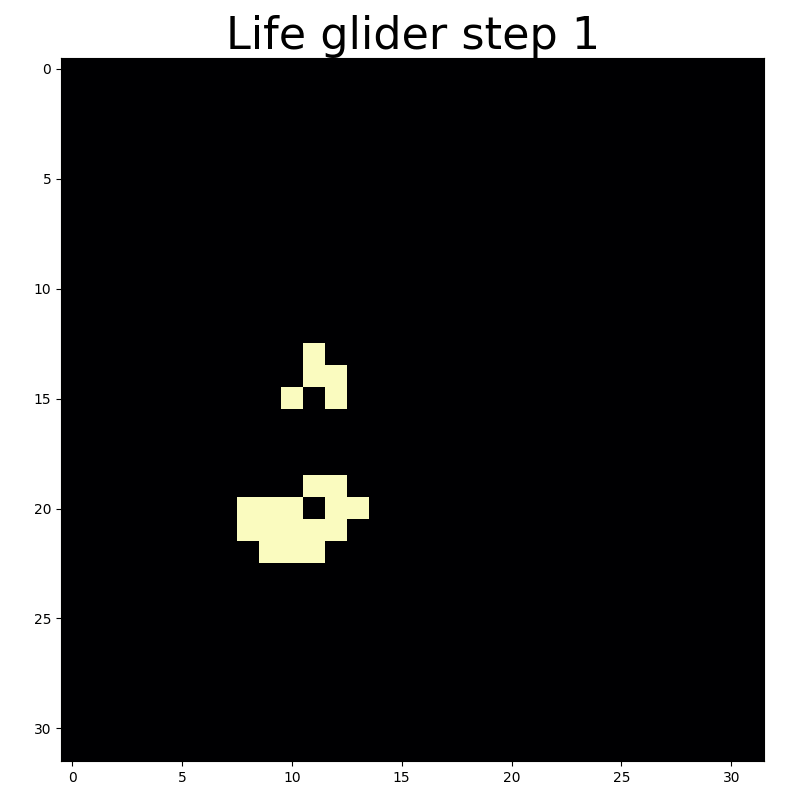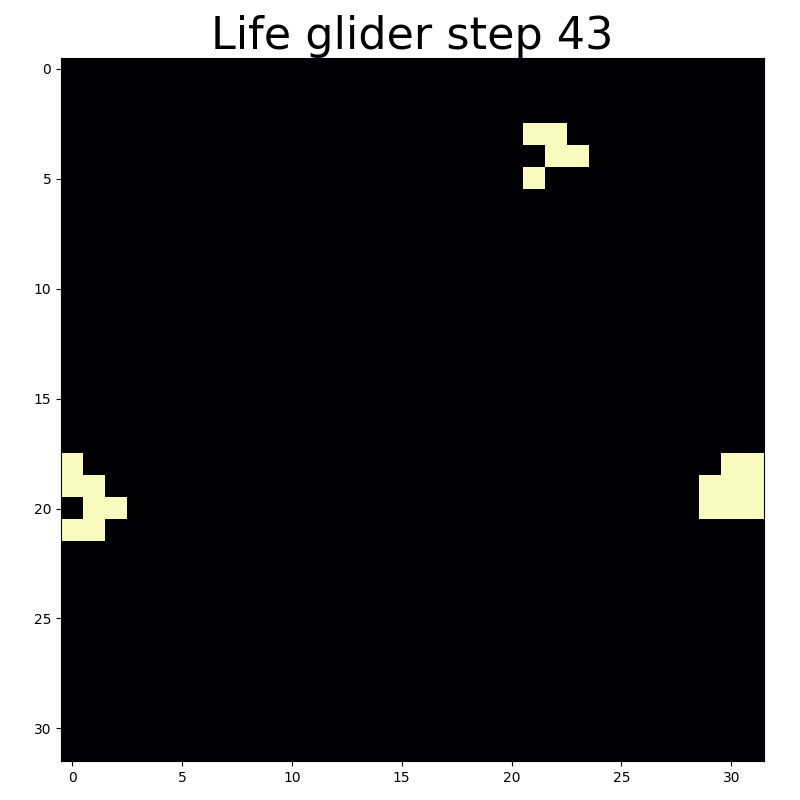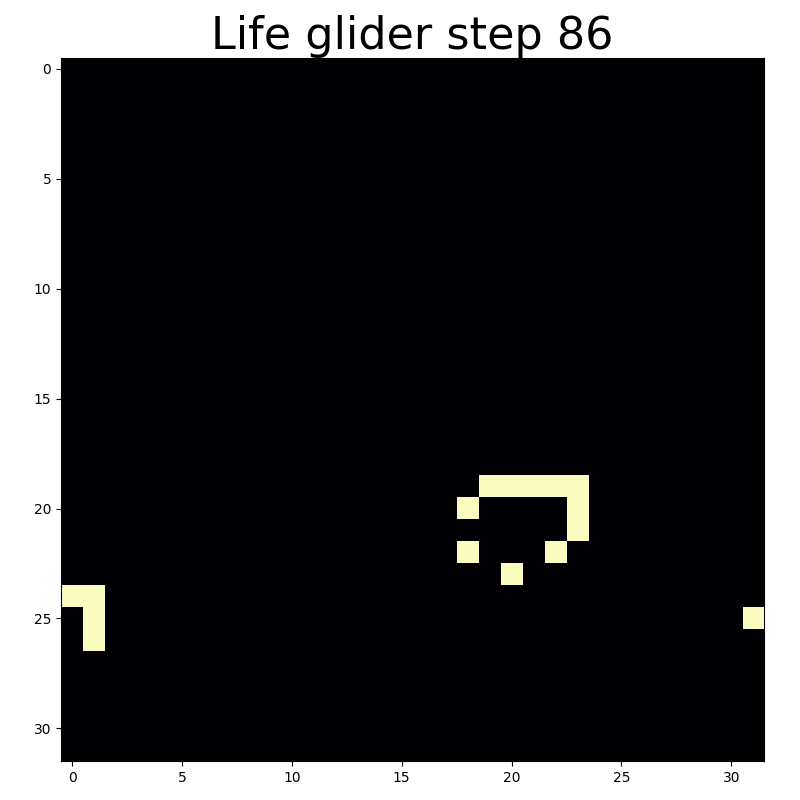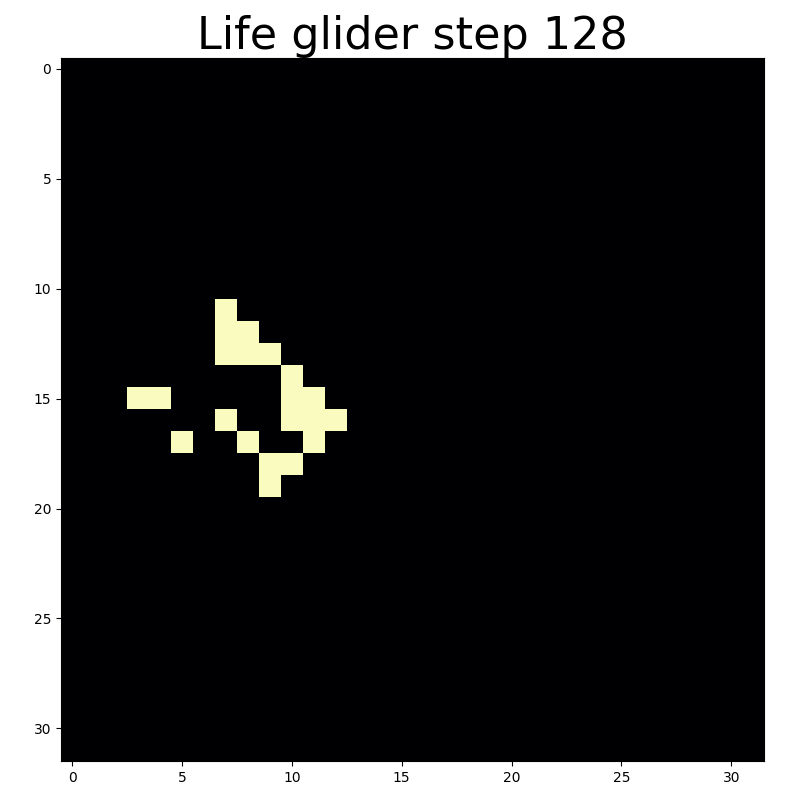
With circular convolutions you can end up back where you started.

Hello There

In a set of previous posts we implemented Life-like cellular automata (CA) in Julia using the Fourier transform convolution theorem, and compared the execution speeds in the Julia language to a similar implemention using NumPy in Python, and to an enhanced CA simulator built using PyTorch, CARLE. Once the bugs had been cleared out, Julia was even faster than the PyTorch CA simulator for a grid size of 64 by 64 cells. Compare to NumPy, Julia was almost always a little faster.

In this post we’ll ditch the convolution theorem and swap out the FFTW.jl Julia package in favor of NNlib.jl, a library implementing many of the neural operations used by the FluxML project. We’ll only be using the convolution operator, NNlib.conv. We’ll be replacing the ft_convolve function

function ft_convolve(grid, kernel)
    
    grid2 = grid 
    
    if size(grid2) != size(kernel)
        padded_kernel = pad_to_2d(kernel, size(grid2))
    else
        padded_kernel = kernel
    end 
    
    convolved = round.(FFTW.ifftshift(abs.(FFTW.ifft(
                    FFTW.fft(FFTW.fftshift(grid2)) .*  
                    FFTW.fft(FFTW.fftshift(padded_kernel)) ))) )
    
    return convolved 
end

with a new function implementing circular convolution with NNlib.conv.

function nn_convolve(grid, kernel)
    
    grid2 = circular_pad(grid)
    
    w = reshape(kernel, (size(kernel)[1], size(kernel)[2], 1,1))
    x = reshape(grid2, (size(grid2)[1], size(grid2)[2], 1,1))

    return conv(x, w, pad=1)[2:end-1,2:end-1,1,1]
end

NNlib.conv doesn’t have a circular padding mode currently, so we will also be replacing a function pad_to_2d that was used to pad the convolution kernel out to match the CA grid dimensions in the Fourier transform implementation. We replace pad_to_2d

function pad_to_2d(kernel, dims)

    padded = zeros(dims)
    mid_x = Int64(round(dims[1] / 2))
    mid_y = Int64(round(dims[2] / 2))
    mid_k_x = Int64(round(size(kernel)[1] / 2))
    mid_k_y = Int64(round(size(kernel)[2] / 2))
    
    start_x = mid_x - mid_k_x
    start_y = mid_y - mid_k_y
    
    padded[2+mid_x-mid_k_x:mid_x-mid_k_x + size(kernel)[1]+1,
            2+mid_y-mid_k_y:mid_y-mid_k_y + size(kernel)[2]+1] = kernel
    
    #padded[1:size(kernel)[1], 1:size(kernel)[2]] = copy(kernel)

    return padded
end

with a new function circular_pad that performs a 1 cell circular padding operation using array indexing.

function circular_pad(grid)
    
    padded = zeros(Float32, size(grid)[1]+2, size(grid)[2]+2)

    padded[2:end-1, 2:end-1] = grid
    
    padded[1, 2:end-1] = grid[end, :]
    padded[end, 2:end-1] = grid[1, :]
    padded[2:end-1, end] = grid[:, 1]
    padded[2:end-1, 1] = grid[:, end]

    padded[1, 1] = grid[end, end]
    padded[end, 1] = grid[1, end] 
    padded[1, end] = grid[end, 1]
    padded[end, end] = grid[1, 1]
   

    return padded
end

Convolution with circular padding essentially wraps the cellular automaton grid around a toroid. This makes for a more interesting universe because moving artifacts that exit the universe via one edge will immediately reappear at the oppositve edge. That’s what enables the midweight spaceship an light glider to wrap back around the universe as they reach the edge.

With the padding and convolution functions replaced, the rest of the code remains the same. With this small update in the way convolutions are performed, the Julia implementation is now nearly 3 times faster than the PyTorch implementation for a 64 by 64 grid, and is about 50% faster at 128 by 128 cells. For an edge dimeension of 256 cells or more, however, CARLE is still faster. The next two tables contain the performance benchmarks for each implementation as they stand now, running the Game of Life with a glider patter for 1000 steps.

Laptop CPU

grid dimensions	Julia FFTW.jl (1 thread)	Julia NNlib.conv	NumPy	CARLE	units
1024 by 1024	5.65	17.85	5.56	46.48	steps/second
256 by 256	162.33	535.56	157.21	877.69	steps/second
128 by 128	882.73	2655.04	641.38	2259.33	steps/second
64 by 64	3292.31	7995.88	1831.78	3280.93	steps/second

Table of execution speeds on a 4-core Intel i5-6300U laptop CPU

Desktop CPU

grid dimensions	Julia FFTW.jl (1 thread)	Julia NNlib.conv	NumPy	CARLE	units
1024 by 1024	6.51	52.28	5.56	263.75	steps/second
256 by 256	159.15	932.74	157.21	1572.89	steps/second
128 by 128	1037.14	4248.94	641.38	2961.82	steps/second
64 by 64	4839.79	12615.08	1831.78	4614.82	steps/second

Table of execution speeds on a 24-core AMD Threadripper 3960x desktop CPU

* As stated in the title, Julia with NNlib.conv is nearly 3 times faster than the PyTorch implementation, CARLE. CARLE still excels for larger grid sizes, and for 1024 by 1024 cells CARLE is more than 5 times faster than Julia, and about 50% faster with a grid size of 256 by 256. While we made substantial improvements in Life-like CA simulation speeds in Julia by switching from a Fourier transform convolution to NNlib.conv, there are still two obvious speedups available. Although not reflected in the performance metrics above, CARLE gets a substantial boost in execution speed by vectorization (computing multiple CA universes in parallel) and hardware acceleration on a GPU. Combined, vectorization and GPU acceleration yields over 100,000 steps per second in CARLE.

GPU acceleration and vectorization combine to yield more than 100,000 steps per second in CARLE, the celluar automata simulator written with PyTorch.

The next lowest-hanging fruit for the cellular automata simulator I described in this post is vectorization. Much like other neural libraries like PyTorch or JAX, NNlib treats adds batch size and channels to 2D matrices. This means we can fairly simply take advantage of the samples dimension to vectorize our convolution operation so that many CA updates can run in parallel. After that the most fruitful speedups will probably be found by investigating GPU support for NNlib. You can take a look at all the code discussed above at https://github.com/rivesunder/life_like.

That’s all for now, thanks for reading. Hope to have you along for the next CA speedup.